RayMarching

记录下ray marching 的笔记

shadertoy中的效果:地址

---

主要参考于这个视频

RayMarching(光线步进) 是从摄像机向屏幕上每一个像素发射一条射线，然后每次按照一定的距离向前方前进，直到到达物体表面。

大致的过程:

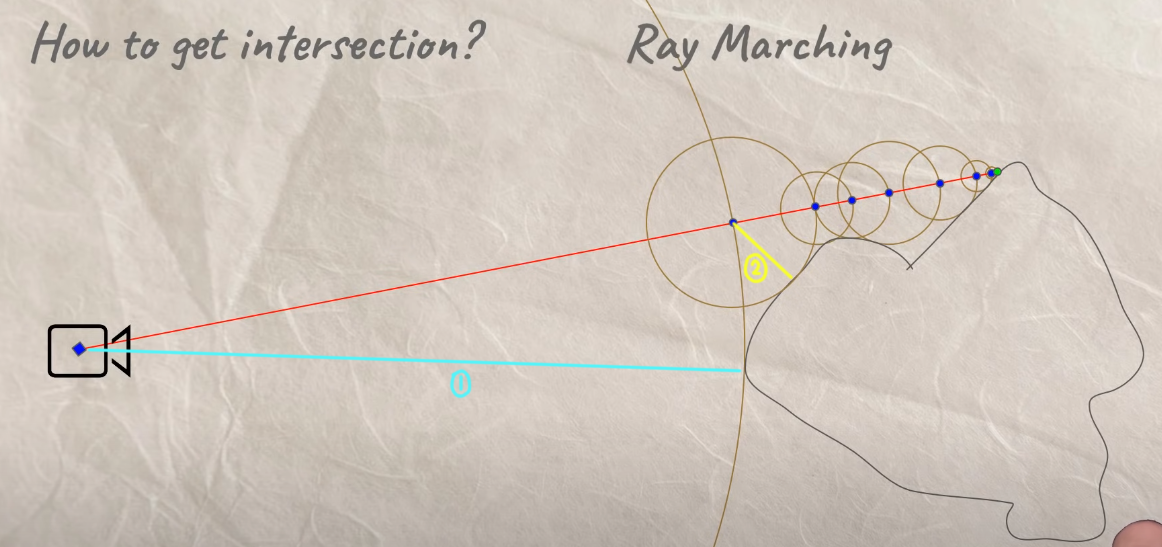
一开始，从摄像机检测到最近的物体，如图蓝色的①线，获取到①的距离dis，这个时候有摄像机的坐标ro，红色射线的方向向量rDir. 就可以求出在射线方向第一次步进后的坐标 (p = ro + rDir * dis) ，之后再从求出的点继续进行检测，如图黄色②线。之后一直这样往下检测，直到抵达物体表面。

先从最简单的开始，在shadertoy中画个球

首先，要实现RayMarch函数，即对每一条射线进行步进，判断是否抵达物体表面，然后返回距离信息

float RayMarch(vec3 ro, vec3 rDir){
    float stepDis = 0.0;
    //Max_Steps是设定的最大步进次数
    for(int i=0; i<Max_Steps; i++){
        // p 点为步进后的坐标
        vec3 p = ro + rDir * stepDis;
        //GetDis获取离p点最近的物体的距离(稍后实现这个函数)
        float tempDis = GetDis(p);
        stepDis += tempDis;
        if(tempDis < 0.01 || stepDis > Max_Dist)
            break;
    }
    return stepDis;
}

那么，GetDis是如何计算p点到最近的物体的距离的？

因为当前场景只有一个球，而且，我们有球的坐标和半径。也有p点的坐标，那么求出p点到球心的距离，再减去球的半径，就得到了p到球最近的距离。

float GetDis(vec3 p){
    //定义一个球,坐标在(0,1,6)
    vec4 sphere = vec4(0, 1, 6, 1);

    //计算点p到球的距离
    float sphereDis = length(p - sphere.xyz) - sphere.w;
    return sphereDis;
}

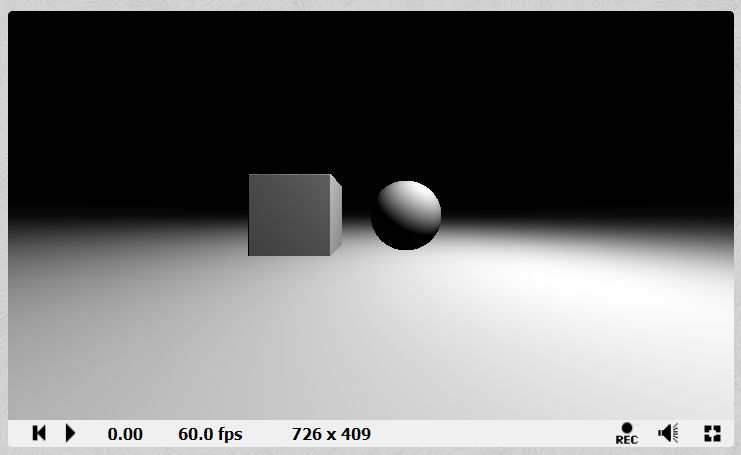
这样，通过对每一条射线进行计算，就可以得到每条射线抵达的深度值，然后在shadertoy中就可以得到上面的深度图了。

完整代码:

#define Max_Steps 100
#define Max_Dist 100.0

float GetDis(vec3 p){
    //定义一个球型,坐标在(0,1,6)
    vec4 sphere = vec4(0, 1, 6, 1);

    //计算点p到球的距离
    float sphereDis = length(p - sphere.xyz) - sphere.w;
    return sphereDis;
}

float RayMarch(vec3 ro, vec3 rDir){
    float stepDis = 0.0;
    for(int i=0; i<Max_Steps; i++){
        vec3 p = ro + rDir * stepDis;
        float tempDis = GetDis(p);
        stepDis += tempDis;
        if(tempDis < 0.01 || stepDis > Max_Dist)
            break;
    }
    return stepDis;
}

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    //把uv坐标限制到(-1,1)
    vec2 uv = (2.0*fragCoord - iResolution.xy)/iResolution.y;
  
    //ro是摄像机坐标
    vec3 ro = vec3(0, 1, 0);
    //rDir是摄像机到每个像素点的方向向量
    vec3 rDir = normalize(vec3(uv.x, uv.y, 1));
  
    float d = RayMarch(ro, rDir);
    d /= 18.0;
    vec3 col = vec3(d);
  
    fragColor = vec4(col,1.0);
}

更进一步，画个长方体

要利用RayMarch画出长方体，就需要求出空间中任意一点到这个长方体的距离

可以通过二维空间中点到的矩形的距离计算来推算出三维的计算公式，可以参考这个视频

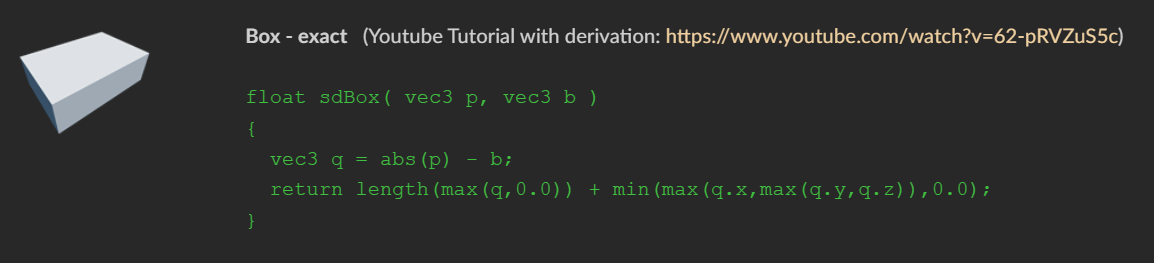
//b是box的长宽高
float BoxDis(vec3 p, vec3 b){
    //设定box的坐标(-2, -1, 6)
    p -= vec3(-2, -1, 6);
    //计算p到box距离
    vec3 q = abs(p) - b;
    float boxDis = length(max(q, 0.0)) + min(max(q.x, max(q.y, q.z)), 0.0);
    return boxDis;
}

float GetDis(vec3 p){
    float sphereDis = SphereDis(p);
    float boxDis = BoxDis(p, vec3(1, 1, 1));
    //比较球和长方体，求出最短距离
    float dis = min(sphereDis, boxDis);
    return dis;
}

完整代码:

#define Max_Steps 100
#define Max_Dist 100.0

float SphereDis(vec3 p){
    //定义一个球型,坐标在(0,1,6)
    vec4 sphere = vec4(1, 1, 6, 1);
    //计算点p到球的距离
    float sphereDis = length(p - sphere.xyz) - sphere.w;
    return sphereDis;
}
//b是box尺寸
float BoxDis(vec3 p, vec3 b){
    //设定box的坐标
    p -= vec3(-2, -1, 6);
    //计算p到box距离
    vec3 q = abs(p) - b;
    float boxDis = length(max(q, 0.0)) + min(max(q.x, max(q.y, q.z)), 0.0);
    return boxDis;
}

float GetDis(vec3 p){
    float sphereDis = SphereDis(p);
    float boxDis = BoxDis(p, vec3(1, 1, 1));

    float dis = min(sphereDis, boxDis);
    return dis;
}

float RayMarch(vec3 ro, vec3 rDir){
    float stepDis = 0.0;
    //Max_Steps是设定的最大步进次数
    for(int i=0; i<Max_Steps; i++){
        // p 点为步进后的坐标
        vec3 p = ro + rDir * stepDis;
        //GetDis获取离p点最近的物体的距离(稍后实现这个函数)
        float tempDis = GetDis(p);
        stepDis += tempDis;
        if(tempDis < 0.01 || stepDis > Max_Dist)
            break;
    }
    return stepDis;
}

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    //把uv坐标限制到(-1,1)
    vec2 uv = (2.0*fragCoord - iResolution.xy)/iResolution.y;
  
    //ro是摄像机坐标
    vec3 ro = vec3(0, 1, 0);
    //rDir是摄像机到每个像素点的方向向量
    vec3 rDir = normalize(vec3(uv.x, uv.y, 1));
  
    float d = RayMarch(ro, rDir);
    d /= 18.0;
    vec3 col = vec3(d);
  
    fragColor = vec4(col,1.0);
}

更多的图形的计算方法可以参考这篇文章，里面有非常多的图形函数

接下来，实现Lambert的漫反射效果

要计算Lambert模型，就需要法线和光的方向。光的方向很容易得到，通过光源坐标减去点的坐标即可，那么法线方向要如何计算?

现在，我们有点的坐标和深度信息，要计算法线，可以在点的位置进行偏移，将它分别向xyz轴偏移一定距离，然后求出偏移后的坐标的深度值，与原点的深度值进行比较，以此求出它在每个方向的偏移量，进行归一化之后就是法线的值了。

vec3 GetNormal(vec3 p){
    float d = GetDis(p);
    //通过偏移量计算normal
    vec3 n = d - vec3(GetDis(p - vec3(0.01, 0, 0)),
                      GetDis(p - vec3(0, 0.01, 0)),
                      GetDis(p - vec3(0, 0, 0.01)));
    return normalize(n);
}

将法线的值输出，就可以得到下面的效果了

有了法线，再设定一个光源的位置，就可以计算出Lambert模型的效果了

//计算漫反射的值
float GetDiff(vec3 p){
    //光源坐标
    vec3 lPos = vec3(3, 5, 3);
    vec3 lDir = normalize(lPos - p);  
    vec3 n = GetNormal(p);

    float diff = dot(n, lDir);
    return diff;
}

阴影

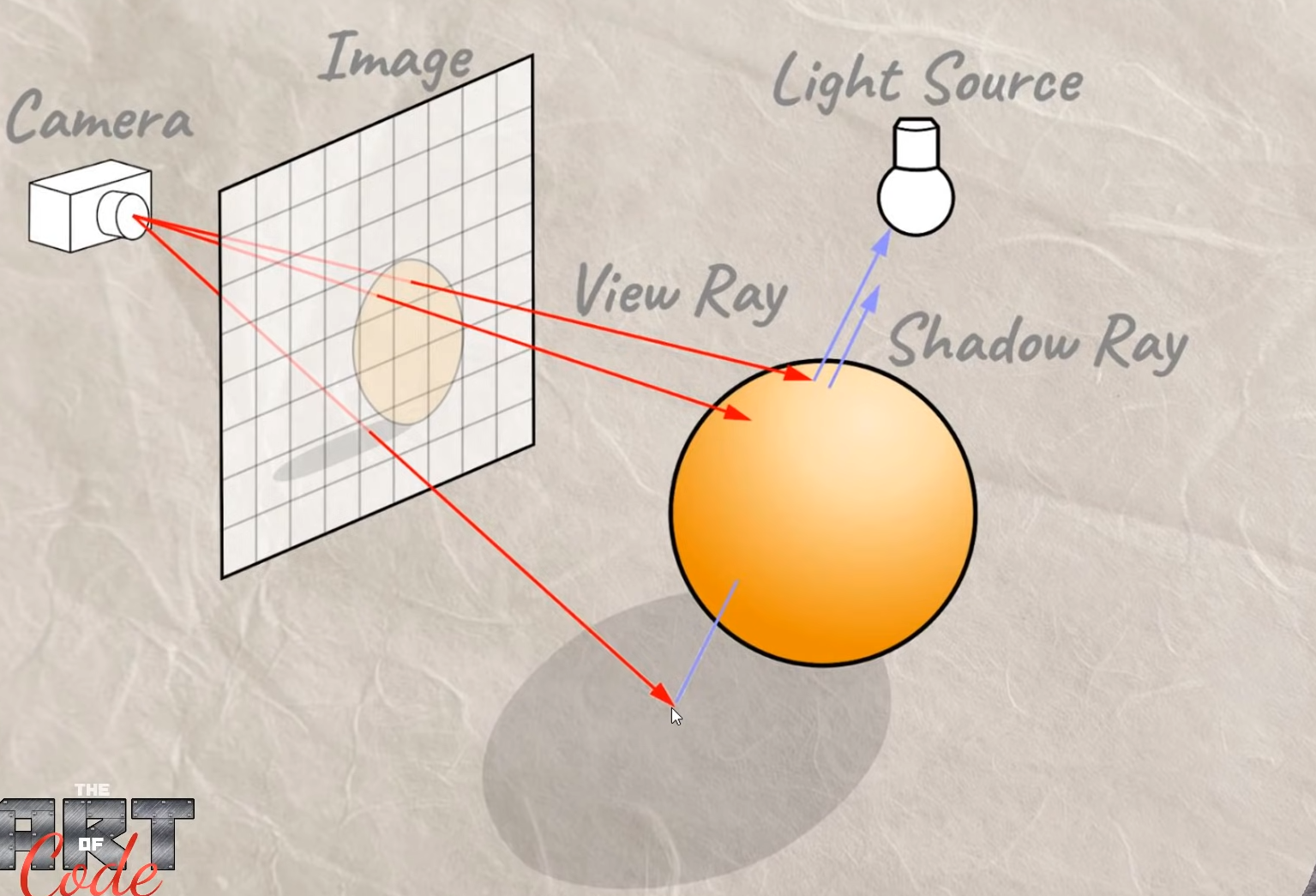
在RayMarching中实现阴影非常方便，只需要在每个点进行一次检测，计算当前点RayMarch到光源的距离，再计算当前点与光源坐标的实际距离，如果RayMarch的距离小于实际距离，那就代表当前的点处于阴影之中。

float GetDiff(vec3 p){
    vec3 lPos = vec3(3, 5, 3);
    //给光源添加一个移动的效果
    lPos.xz += vec2(sin(iTime), cos(iTime)) * 3.0;

    vec3 lDir = normalize(lPos - p);
    vec3 n = GetNormal(p);

    float diff = clamp(dot(n, lDir), 0.0, 1.0);

    //shadow
    float p2lDis = RayMarch(p + n * 0.02, lDir);
    if(p2lDis < length(lPos - p))
        diff *= 0.1;
  
    return diff;
}

MetaBall

通过opSmoothUnion函数实现物体之间的融合效果

d1,d2分别为当前点到要融合物体的距离，k为参数值，k值越大融合的效果更明显

//光滑混合
float opSmoothUnion(float d1, float d2, float k){
    float h = clamp( 0.5 + 0.5*(d2-d1)/k, 0.0, 1.0 );
    return mix( d2, d1, h ) - k*h*(1.0-h);
}

float GetDis(vec3 p){
    float sphereDis = SphereDis(p);
    float boxDis = BoxDis(p, vec3(1, 1, 1));
    //融合
    float combine = opSmoothUnion(sphereDis, boxDis, 0.8);

    float dis = min(combine, p.y);
    dis = min(dis, boxDis);
    return dis;
}

完整代码:

#define Max_Steps 100
#define Max_Dist 100.0

float SphereDis(vec3 p){
    //定义一个球型,坐标在(0,1,6)
    vec4 sphere = vec4(1, 1, 4, 1);
    sphere.x += sin(iTime) * 2.0;
    //计算点p到球的距离
    float sphereDis = length(p - sphere.xyz) - sphere.w;
    return sphereDis;
}
//b是box尺寸
float BoxDis(vec3 p, vec3 b){
    //设定box的坐标
    p -= vec3(-2, 1, 4);
    //计算p到box距离
    vec3 q = abs(p) - b;
    float boxDis = length(max(q, 0.0)) + min(max(q.x, max(q.y, q.z)), 0.0);
    return boxDis;
}

//光滑混合
float opSmoothUnion(float d1, float d2, float k){
    float h = clamp( 0.5 + 0.5*(d2-d1)/k, 0.0, 1.0 );
    return mix( d2, d1, h ) - k*h*(1.0-h);
}

float GetDis(vec3 p){
    float sphereDis = SphereDis(p);
    float boxDis = BoxDis(p, vec3(1, 1, 1));
    //融合
    float combine = opSmoothUnion(sphereDis, boxDis, 0.8);

    float dis = min(combine, p.y);
    dis = min(dis, boxDis);
    return dis;
}

vec3 GetNormal(vec3 p){
    float d = GetDis(p);
    //通过偏移量计算normal
    vec3 n = d - vec3(GetDis(p - vec3(0.01, 0, 0)),
                      GetDis(p - vec3(0, 0.01, 0)),
                      GetDis(p - vec3(0, 0, 0.01)));
    return normalize(n);
}

float RayMarch(vec3 ro, vec3 rDir){
    float stepDis = 0.0;
    //Max_Steps是设定的最大步进次数
    for(int i=0; i<Max_Steps; i++){
        // p 点为步进后的坐标
        vec3 p = ro + rDir * stepDis;
        //GetDis获取离p点最近的物体的距离(稍后实现这个函数)
        float tempDis = GetDis(p);
        stepDis += tempDis;
        if(tempDis < 0.01 || stepDis > Max_Dist)
            break;
    }
    return stepDis;
}

float GetDiff(vec3 p){
    vec3 lPos = vec3(3, 8, 3);
    //
    lPos.xz += vec2(sin(iTime), cos(iTime)) * 3.0;

    vec3 lDir = normalize(lPos - p);  
    vec3 n = GetNormal(p);

    float diff = clamp(dot(n, lDir), 0.0, 1.0);

    //shadow
    float p2lDis = RayMarch(p + n * 0.02, lDir);
    if(p2lDis < length(lPos - p))
        diff *= 0.1;
  
    return diff;
}

void mainImage( out vec4 fragColor, in vec2 fragCoord)
{
    //把uv坐标限制到(-1,1)
    vec2 uv = (2.0*fragCoord - iResolution.xy)/iResolution.y;
  
    //ro是摄像机坐标
    vec3 ro = vec3(0, 1, 0);
    //rDir是摄像机到每个像素点的方向向量
    vec3 rDir = normalize(vec3(uv.x, uv.y, 1));
  
    float d = RayMarch(ro, rDir);
    vec3 p = ro + d * rDir;
    float diff = GetDiff(p);

    vec3 col = vec3(diff);
  
    fragColor = vec4(col,1.0);
}